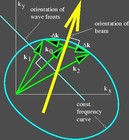
Rigorously, all vector fields are two-point functions and thus decomposable into two scalar fields, as Whittaker showed in 1903. It follows that any vector wave can be decomposed into two scalar waves. By implication, therefore, a normal transverse E

Electronica experimental
Influenced by kraftwerk from Germany and the
History Channel
Story behind the song
Rigorously, all vector fields are two-point functions and thus decomposable into two scalar fields, as Whittaker showed in 1903. It follows that any vector wave can be decomposed into two scalar waves. By implication, therefore, a normal transverse EM vector wave, e.g., must simply be two coupled scalar (Tesla) waves -- and these scalars independently would be longitudinal if uncoupled. An ordinary transverse EM vector wave is thus two pair-coupled Tesla scalar longitudinal waves, and only a single special case of the much more fundamental electromagnetics discovered by Nikola Tesla
Lyrics
Rigorously, all vector fields are two-point functions and thus decomposable into two scalar fields, as Whittaker showed in 1903. It follows that any vector wave can be decomposed into two scalar waves. By implication, therefore, a normal transverse EM vector wave, e.g., must simply be two coupled scalar (Tesla) waves -- and these scalars independently would be longitudinal if uncoupled. An ordinary transverse EM vector wave is thus two pair-coupled Tesla scalar longitudinal waves, and only a single special case of the much more fundamental electromagnetics discovered by Nikola Tesla